The `Monks Equations' are a set of differential equations in four variables, which describe interacting waves on an annulus.

The original equations are complex and non-analytic; they should have complex conjugate operators in them. However, Bertini (and the underlying mathematical theory) only work for analytic functions, so in order to work with them, we drop the bar operator, and are left with a set of real equations.

Running the above input file yields some pretty cool data. One of the primary features of this system is that the number of real solutions varies throughout parameter space:

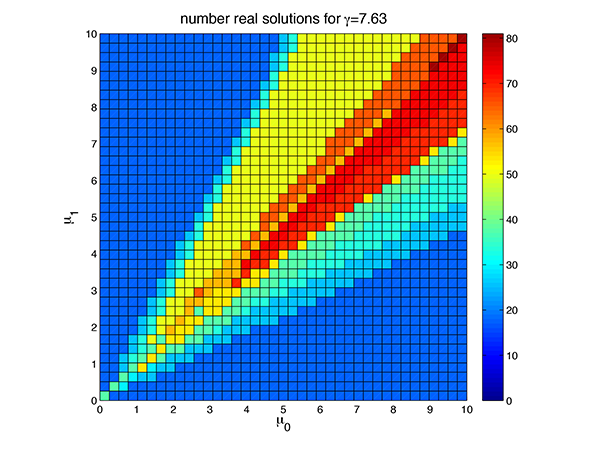
The number of real solutions varies through the parameter space. The above is a slice for $\gamma = 7.63$.

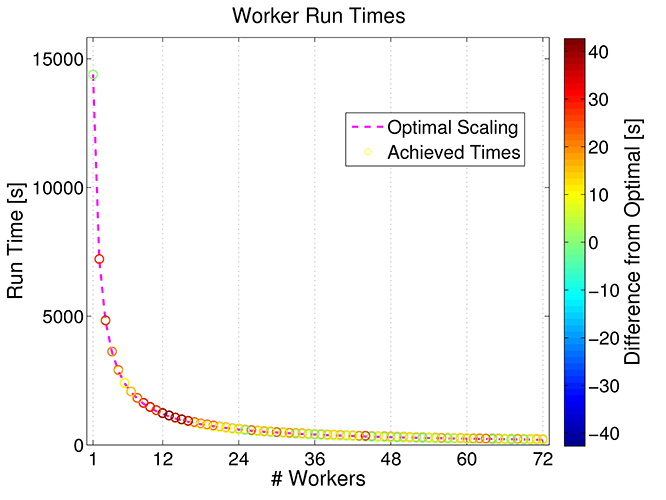
Using the monks equations as a benchmark for testing scaling performance with Paramotopy, we see nice $1/n$ dropoff for time versus the number of workers used to perform the work.

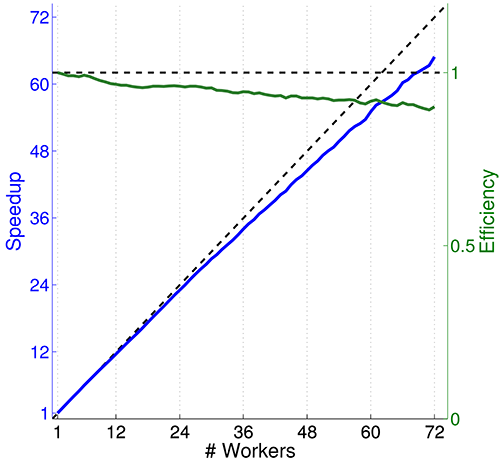
Speedup and efficiency versus number of workers. Performance curves indicate we had not yet reached the peak performance of Paramotopy.