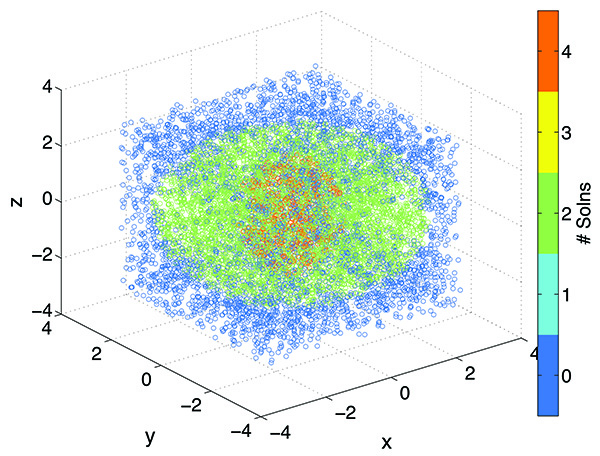
Running the above input file, and using a 10000 point random sampling of the box $[-3, 3]^3$, we get the above scatterplot, describing the sampling space in terms of the number of solutions Bertini finds. In the center, we find an orange cylinder-like object having the full number of solutions, which is four. Around this is a green region where the manipulator would be able to reach the point in two ways. The blue region is unreachable.

Note that each of these points actually has four solutions, regardless of the color of the point above. Bertini solves over the complex numbers $\mathbb{C}^n$, and Bertini's Theorem guarantees that off a set of measure zero, the system will have an identical number of solutions. This is true in the case of the kinematic manipulator here, so if we had plotted the number of complex solutions at each point, the plot would be uniformly orange.